| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 |
- 12기
- sk네트웍스ai캠프
- 헤더가드
- Docker
- 최종프로젝트
- C++
- Fine-tuning
- few-shot
- zero-shot
- sk네트웍스familyai캠프12기
- Rag
- one-shot
- sk네트웍스familyai캠프
- openai
- 어셈블
- 링크
- 회고록
- 주간회고
- FastAPI
- sk네트웍스family
- 중복인클루드
- 임베딩
- 전처리
- Langchain
- AWS
- 컴파일
- 소스코드
- 배포
- ai캠프
- #include
- Today
- Total
ansir 님의 블로그
SK 네트웍스 family AI 캠프 6주차 회고( 2025-03-31 ~ 2025-04-04 ) 본문
SK 네트웍스 family AI 캠프 6주차 회고( 2025-03-31 ~ 2025-04-04 )
ansir 2025. 4. 8. 17:03
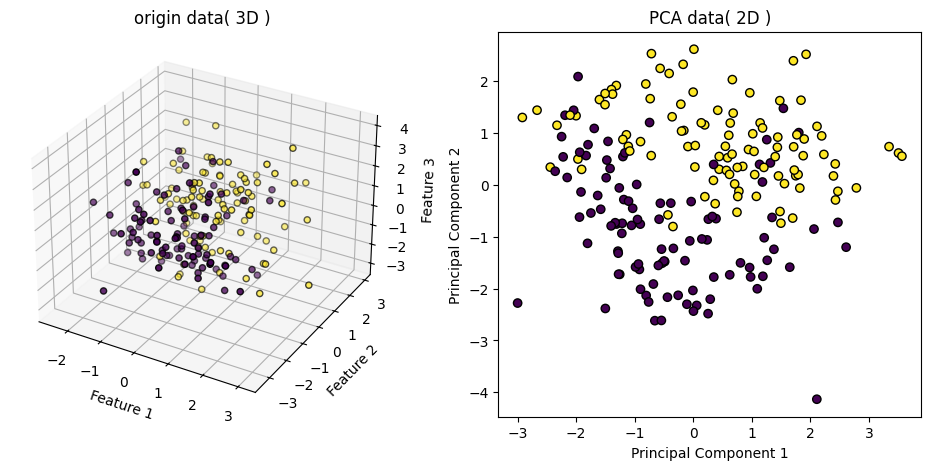
PCA
PCA( Principal Component Analysis )는 고차원 데이터를 저차원으로 압축하면서도, 데이터의 변동성( 정보 )은 최대한 보존하는 차원 축소 기법입니다.
주요 아이디어는 데이터를 가장 잘 설명하는 방향( 축 )을 새로 만들어서, 그 축을 기준으로 데이터를 다시 표현하고, 덜 중요한 축은 잘라내는 것입니다.
데이터 컬럼이 너무 많을 때 줄여주는 기능을 하며 전체 이미지 주성분을 분석할 때에는 주 이미지 주변에 있는 작고 필요없는 픽셀들이 제거가 되어 노이즈를 제거하는 효과도 있습니다.
차원을 줄인 후에도 원래 차원으로 복원할 수 있으며, 얼마나 잘 압축이 되어 있는지 설명된 분산 비율( explained variance ratio )로 알 수 있습니다. 이를 누적해서 보면 "몇 개의 주성분이 전체 정보의 몇 %를 설명하는가"를 알 수 있습니다.
인공 신경망
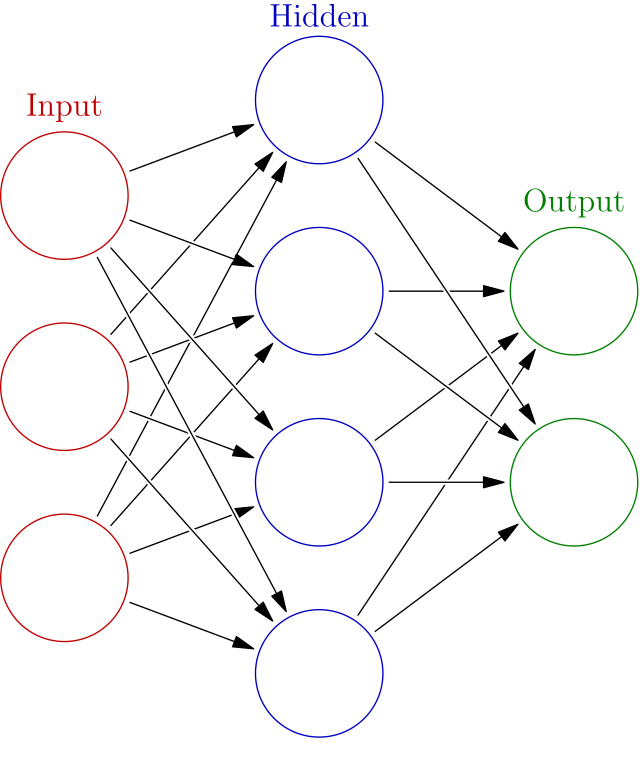
생물학적 뉴런에서 영감을 받아 만든 머신러닝 알고리즘입니다.
입력층( Input ), 은닉층( Hidden ), 출력층( Output )으로 이루어져 있으며, 신경망 내부에 선으로 연결된 부분을 밀집층( dense )라고 합니다.
데이터가 들어오고 입력층에서 출력 층으로 이동되면서 결과가 도출되며, 신경망은 출력층 데이터가 또 다른 밀집층의 입력층으로 들어가는 것을 반복하게 됩니다.
심층 신경망

활성 함수
뉴런의 선형 방정식 계산 결과에 적용되는 함수입니다.
신경망의 레이어를 설계하다보면 각 층마다 활성 함수를 다르게 사용합니다.
은닉층 ReLU (relu)
tf.keras.layers.Dense(10, activation='relu')- ReLU (Rectified Linear Unit) 함수는 **max(0, x)*로 정의됩니다.
- 즉, 음수 값은 0으로 만들고, 양수 값은 그대로 둡니다.
- 비선형성을 추가해서 신경망이 복잡한 패턴을 학습할 수 있도록 도와줍니다.
출력층 Sigmoid (sigmoid)
tf.keras.layers.Dense(1, activation='sigmoid')- Sigmoid 함수는 출력을 확률로 변환하는 역할입니다.
- 출력값이 0~1 사이로 제한되므로 이진 분류(Binary Classification)에 적합.
출력층 Softmax (softmax)
tf.keras.layers.Dense(1, activation='softmax')- softmax 함수도 출력을 확률로 변환하는 역할을 합니다.
- 모든 출력값을 0~1 사이의 값으로 바꿔주고, 합이 1이 되도록 만들기 때문에 다중 분류 문제에 적합합니다.
손실함수
- 모델의 예측값과 실제값 사이의 차이를 구할 수 있는 함수입니다.
- loss 값( 손실값 )이 작을수록 모델이 실제 정답에 가까운 예측을 하고 있다는 의미입니다.
- loss 함수는 문제 유형에 따라 다르게 설정됩니다.
문제 유형손실 함수 (loss)
| 이진 분류 | binary_crossentropy |
| 다중 분류 | categorical_crossentropy 또는 sparse_categorical_crossentropy |
| 회귀 문제 | mse (Mean Squared Error) 또는 mae (Mean Absolute Error) |
합성곱 신경망
합성곱은 입력 데이터에 마치 도장을 찍어서 유용한 특성만 드러나게 하는 것 비유할 수 있습니다.
- 이미지 + 필터(커널) → 특징맵(feature map) 생성
- 필터는 작은 크기의 행렬이고, 이미지를 슬라이딩하면서 곱셈 + 덧셈을 합니다.
- 이 연산 결과로 특정 패턴이 있는 곳에 높은 값, 아닌 곳엔 낮은 값을 줍니다.
패딩
합성곱 층의 입력 주위에 추가한 0으로 채워진 픽셀입니다.

스트라이드
합성곱 층에서 필터가 입력 위를 이동하는 크기입니다.

풀링
가중치가 없고 특성 맵의 가로세로 크기를 줄이는 역할을 수행합니다.
순환 신경망과 LSTM
순환 신경망( RNN, REcurrent Neural Network )
RNN은 과거의 정보를 기억하면서 다음 출력을 계산할 수 있다는 특징이 있어서 시퀀스 데이터를 처리하는 데 쓰입니다.
- 텍스트 (문장)
- 음성
- 시간에 따른 센서 데이터
RNN의 한계
1️ 기울기 소실 (Vanishing Gradient)
- 경사 하강법을 사용할 때, 가중치가 점점 작아져서 0에 수렴하면 학습이 멈춥니다.
- 특히, 긴 문장이나 시퀀스를 학습할 때 초반 데이터가 사라지는 문제가 발생합니다.
2️ 기울기 폭발 (Exploding Gradient)
- 가중치가 계속 더해지면서 값이 커지면 네트워크가 불안정해질 수 있습니다.
- 출력 값이 급격하게 변화하는 현상이 발생합니다.
3️ 해결 방법: 기울기 클리핑 (Gradient Clipping)
- numpy의 클리핑 함수를 사용하여 가중치를 일정 범위로 제한하는 방법이 있습니다.
- 하지만 이는 근본적인 해결책은 아닙니다.
LSTM( Long Short-Term Memory )의 등장
LSTM은 RNN의 단점을 보완하기 위해 만들어졌으며, 기억을 유지하거나 잊을 수 있도록 설계되었습니다.
이를 위해 게이트(Gate)와 셀(Cell) 구조를 도입하였습니다.
LSTM의 핵심 개념
게이트 (Gate)
게이트는 어떤 정보를 유지할지 버릴지를 결정합니다.
LSTM에는 망각 게이트, 입력 게이트, 출력 게이트가 존재합니다.
1️ 망각 게이트 (Forget Gate)
- 불필요한 정보 제거
- 값이 0에 가까우면 잊고, 1에 가까우면 유지
2️ 입력 게이트 (Input Gate)
- 새로운 정보를 기억할지 결정
3️ 출력 게이트 (Output Gate)
- 최종적으로 어떤 정보를 은닉 상태(hidden state)로 전달할지 결정
LSTM의 동작 과정
1️ 이전 시점의 정보와 새로운 정보를 비교하여 불필요한 정보는 버림 (망각 게이트)
2️ 새로운 정보를 추가할지 결정 (입력 게이트)
3️ 최종적으로 어떤 정보를 다음 단계로 전달할지 결정 (출력 게이트)
밀집 벡터(Dense Vector)
벡터는 숫자들의 리스트를 말합니다.
여기에서 "밀집"이란 건, 대부분의 원소가 0이 아닌 값을 갖는 걸 말합니다.
예를 들어:
csharp
[0.13, -0.28, 0.91, 0.07, -0.64]
위처럼 숫자가 다양하게 섞여있고, 대부분 0이 아닌 벡터가 밀집 벡터입니다.
반대로 대부분이 0인 벡터는 "희소 벡터(Sparse Vector)"라고 합니다. ( 예: One-hot encoding )
단어 임베딩(Word Embedding)
단어를 컴퓨터가 이해할 수 있게 하려면 숫자로 바꿔줘야 합니다.
하지만 그냥 숫자로 바꾸게 되면 의미가 없습니다.( 예: "apple" → 3 )
이 때 사용할 수 있는게 단어 임베딩입니다.
단어 임베딩은 단어를 밀집 벡터 형태로 표현하면서, 의미까지 반영합니다.
로직스틱 회귀( Logistic Regression )
이진 분류 문제에서 가장 기본적이고 중요한 모델
쉽게 말하면 어떤 일이 발생할 확률을 예측해주는 모델입니다.
선형 회귀처럼 생겼지만 결과는 확률
로지스틱 회귀는 먼저 선형 회귀처럼 가중치와 입력값의 곱을 계산한 후에,
이 값을 시그모이드 함수에 통과시켜 0~1 사이 확률 값으로 바꿔줍니다.
시그모이드 함수
0~1 사이의 값으로 변환하는 방법
신경망에서 뉴런의 출력은 입력값과 가중치( weight )의 선형 조합 + 편향( bias ) 으로 계산됩니다.
이를 확률처럼 해석할 수 있는 값으로 변환해야 하는데 이때 사용하는 게 바로 시그모이드(sigmoid) 함수입니다.
시그모이드 함수 적용

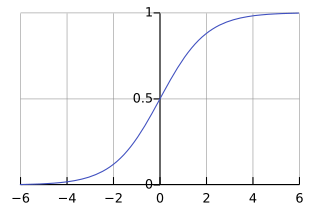
[출처] https://ko.wikipedia.org/wiki/%EC%8B%9C%EA%B7%B8%EB%AA%A8%EC%9D%B4%EB%93%9C_%ED%95%A8%EC%88%98
시그모이드 함수를 적용시키면 아무리 큰 값이 들어와도 1을 넘을 수 없고, 아무리 작은 값이 들어와도 0보다 작아질 수 없습니다.
Isolation Forest
핵심 아이디어
"이상치는 정규 데이터보다 고립시키기 쉬우며, 이 고립 정도를 이용해 이상치를 탐지한다."
아래와 같은 데이터가 있다고 가정해봅니다.
정상값: 50, 51, 52, 53, 54
이상값: 100
이제 IsolationForest는 이 값들 사이에 무작위로 분할점(cut point) 을 만듭니다.
예시:
- [0, 105] 범위에서 랜덤하게 하나의 값을 선택해서 "이 값보다 작으면 왼쪽, 크면 오른쪽"으로 나눕니다.
- 예를 들어 60에서 잘랐을 때
- 50~54는 전부 왼쪽
- 100은 오른쪽 혼자 → 고립
이 과정을 여러 번 반복하면서,
"몇 번만에 고립되는지"를 확인합니다.
- 정상 데이터는 여러 번 나눠야 고립됩니다
- 이상치는 몇 번 안에 바로 고립되기 때문에 이상치로 판단합니다.
스케일링 기법
| 스케일링 기법 | 변환 방식 | 특징 |
|---|---|---|
| StandardScaler | 평균 0, 표준편차 1로 변환 | 이상치에 민감함 |
| MinMaxScaler | [0, 1] 범위로 변환 | 이상치의 영향이 큼 |
| RobustScaler | 중간값 0, IQR(사분위 범위)로 조정 | 이상치에 강함 |
| Normalizer | 벡터 크기(길이)를 1로 정규화 | 거리 기반 모델에 적합 |
SelectKBest
SelectKBest는 특성 선택(Feature Selection) 기법 중 하나로,
각 특성(컬럼)의 중요도를 평가하여 상위 k개의 특성만 선택하는 방법입니다.
동작 과정
- 각 특성과 타겟 변수(y) 간의 관계를 평가합니다.
- 특정 기준(예: ANOVA F-통계량, 카이제곱 통계량 등)으로 중요도를 측정합니다.
- 가장 중요한 상위 k개의 변수만 선택합니다.
결과적으로 모델 성능 향상을 위해 중요한 변수만 남기고, 덜 중요한 변수는 제거하게 됩니다.
파이프라인( Pipeline )
파이프라인은 여러 개의 데이터 전처리 과정과 모델을 하나로 묶어서 실행하는 기능으로,
데이터 전처리 → 특성 선택 → 모델 학습을 하나의 흐름(파이프라인)으로 처리할 수 있습니다.
KPT
- Keep : 현재 만족하고 있는 부분, 계속 이어갔으면 하는 부분
- Problem : 불편하게 느끼는 부분, 개선이 필요하다고 생각되는 부분
- Try : Problem에 대한 해결책, 실행 가능한 것
Keep
자투리 시간 활용( 인프런 강의, 부교재 공부 )
이동 시간과 쉬는 시간에 틈틈히 인프런 강의와 부교재를 보며 공부하고 있습니다. 지난주 데이터 분석을 지나 머신 러닝 파트가 되니 수업 진도가 엄청 빨라졌습니다. 수업 시간 때 개념적인 부분이 부족해서 이해하지 못했던 부분들을 위주로 공부하고 있습니다.
ai 툴 활용( cursor, chat gpt )
머신 러닝과 딥러닝은 매우 다양한 알고리즘과 모델들이 있지만 다행히 그 구조는 비슷합니다. ai IDE cursor와 chat gpt를 활용하여 다양한 예제를 받고 따라해보면서 그 구조를 익히기 위해 노력하고 있습니다.
Problem
판다스, numpy 개념 부족
머신러닝의 이론적인 부분은 이해했지만 막상 모델을 훈련하려고 데이터 분석을 할 때 뭐부터 해야할지 감을 못잡을 때가 많습니다. 그 이유는 판다스와 넘파이의 구조를 제대로 파악하지 못했기 때문이라는 생각이 큽니다.
Try
인프런 강의와 부교재로 판다스 공부하기
adsp 자격증 공부 시작하기
'SK 네트웍스 family AI 캠프 > 주간 회고' 카테고리의 다른 글
| SK 네트웍스 family AI 캠프 8주차 회고( 2025-04-14 ~ 2025-04-18 ) (0) | 2025.04.22 |
|---|---|
| SK 네트웍스 family AI 캠프 7주차 회고( 2025-04-07 ~ 2025-04-11 ) (1) | 2025.04.14 |
| SK 네트웍스 family AI 캠프 5주차 회고( 2025-03-24 ~ 2025-03-28 ) (0) | 2025.03.31 |
| SK 네트웍스 family AI 캠프 4주차 회고( 2025-03-17 ~ 2025-03-21 ) (0) | 2025.03.24 |
| SK 네트웍스 family AI 캠프 3주차 회고( 2025-03-10 ~ 2025-03-14 ) (0) | 2025.03.18 |





